
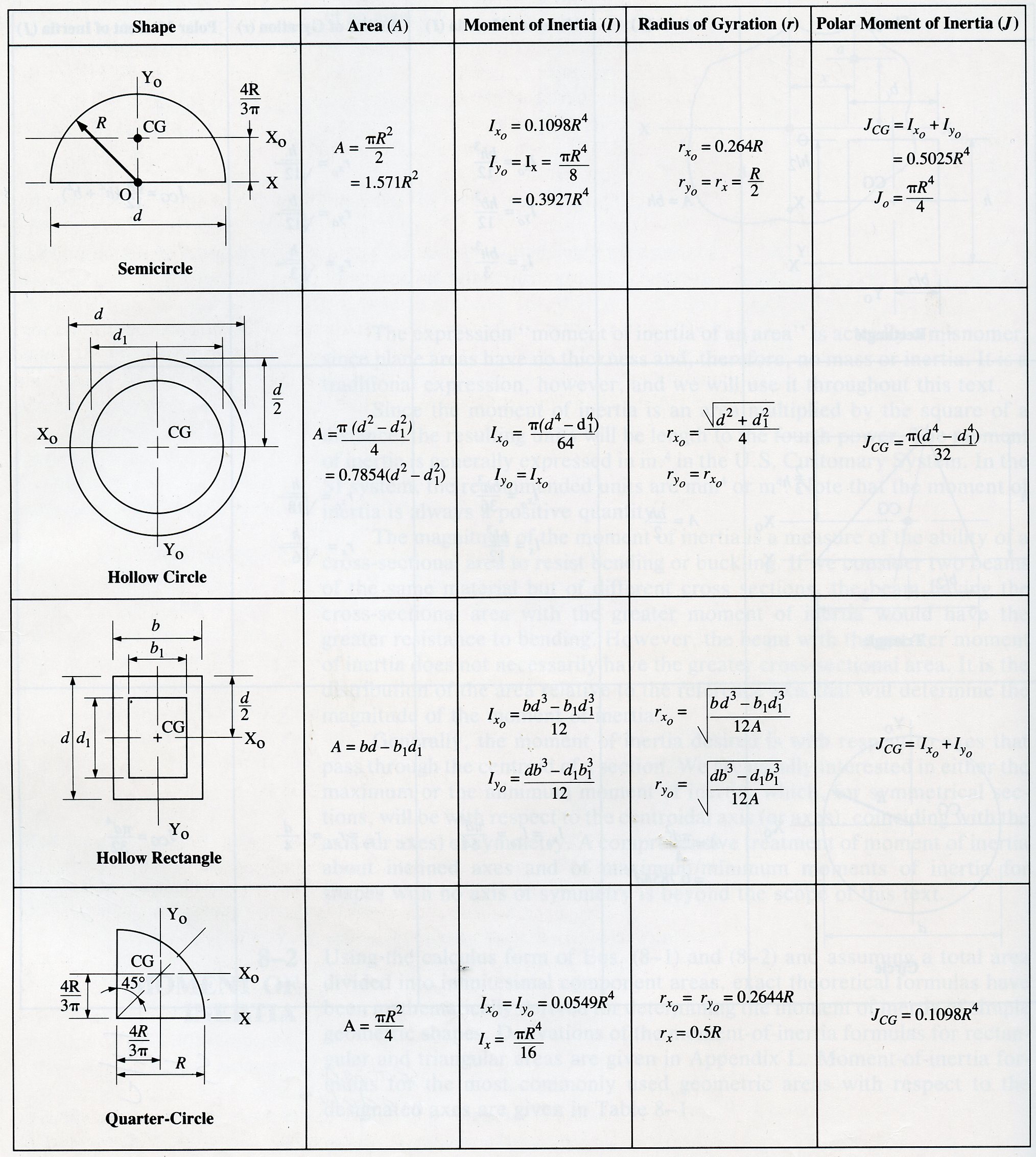
Integrating curvatures over beam length, the deflection, at some point along x-axis, should also be reversely proportional to I. Here are the formulae of the second moment of inertias of standard shapes: The second moment of inertia calculation of rectangular cross-section So, as you see, the area moment of inertia of rectangular cross-sections for X and Y axes are defined above. cantilever and over hanging beams Moment of area and moment of inertia for rectangular. The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure (see beam bending theory). 2, Border Road Organization (BRO), Junior Engineer (Electrical &. Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. The term second moment of area seems more accurate in this regard. If you’re having difficulty determining the second moment of area of a hexagon, a circle or any other common shape, this moment of inertia calculator can help you out. Where Ixy is the product of inertia, relative to centroidal axes x,y, and Ixy' is the product of inertia, relative to axes that are parallel to centroidal x,y ones, having offsets from them d_. The formula for calculating the moment of inertia can be derived as, and as a result, the moment-curvature relation. Area Moment of Inertia or Moment of Inertia for an Area - also known as Second Moment of Area - I, is a property of shape that is used to predict deflection, bending and stress in beams. Second Moment of Area is defined as the capacity of a cross-section to resist bending. Second Moment of Area Calculator for I beam, T section, rectangle, c channel, hollow rectangle, round bar and unequal angle. Where I' is the moment of inertia in respect to an arbitrary axis, I the moment of inertia in respect to a centroidal axis, parallel to the first one, d the distance between the two parallel axes and A the area of the shape (=bh in case of a rectangle).įor the product of inertia Ixy, the parallel axes theorem takes a similar form: The second moment of area, also referred to as the moment of inertia, is used as a measure to evaluate the flexural rigidity of a section and also to calculate the deflections, flexural stresses, and shear stresses of structures. The following is a list of second moments of area of some shapes. SECOND MOMENT OF AREA (AREA MOMENT OF INERTIA) CALCULATOR. The so-called Parallel Axes Theorem is given by the following equation: The moment of inertia of any shape, in respect to an arbitrary, non centroidal axis, can be found if its moment of inertia in respect to a centroidal axis, parallel to the first one, is known.


 0 kommentar(er)
0 kommentar(er)
